Chebfun Notes
https://www.chebfun.org/docs/guide
Each smooth piece is mapped to the interval [−1, 1] and represented by an expansion in Chebyshev polynomials of the form
\[f_N(x)=\sum_{j=0}^N \lambda_j T_j(x), \quad x \in[-1,1]\]where $T_j(x)=\cos (j \arccos (x))$. When constructing a fun object, the system computes the coefficients λj by interpolating the target function f at N + 1 Chebyshev extreme points
\[x_j=\cos \frac{\pi j}{N}, \quad j=0, \ldots, N\]The polynomial degree N is automatically determined so that the representation is as accurate as possible in double precision arithmetic.
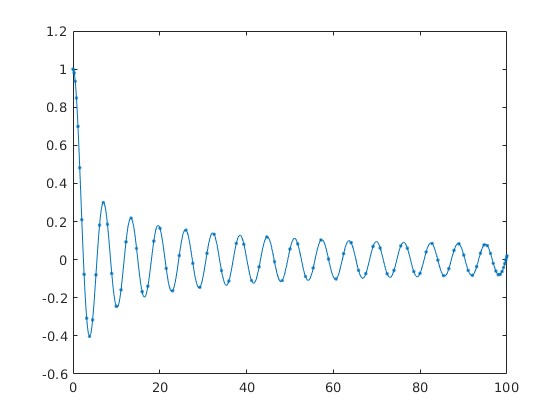
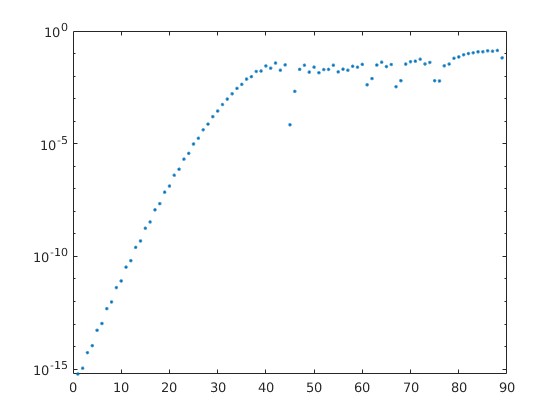
Barycentric Lagrange Interpolation1
Lagrange form
\[p(x)=\sum_{j=0}^n f_j \ell_j(x), \quad \ell_j(x)=\frac{\prod_{k=0, k \neq j}^n\left(x-x_k\right)}{\prod_{k=0, k \neq j}^n\left(x_j-x_k\right)}, \quad \ell_j\left(x_k\right)=\left\{\begin{array}{ll} 1, & j=k, \\ 0, & \text { otherwise }, \end{array} \quad j, k=0, \ldots, n\right.\]first form of the barycentric interpolation formula:
\[p(x)=\ell(x) \sum_{j=0}^n \frac{w_j}{x-x_j} f_j\]barycentric formula (second form of the barycentric formula)
\[p(x)=\frac{\sum_{j=0}^n \frac{w_j}{x-x_j} f_j}{\sum_{j=0}^n \frac{w_j}{x-x_j}}\]Runge phenomenon is not a problem with the barycentric formula, but is intrinsic in the underlying interpolation problem.
Chebyshev points of the first kind:
\[x_j=\cos \frac{(2 j+1) \pi}{2 n+2}, \quad j=0, \ldots, n\]Chebyshev points of the second kind:
\[x_j=\cos \frac{j \pi}{n}, \quad j=0, \ldots, n\]