CITE https://mujoco.readthedocs.io/en/latest/modeling.html#solver-parameters

Impedance

The impedance $d\in (0,1)$ determines a constraint’s ability to generate force. Small values of $d$ correspond to weak constraints while large values of $d$ correspond to strong constraints. Impedance is set using the solimp attribute.

Recall that $d$ must lie between 0 and 1; internally MuJoCo clamps it to the range [mjMINIMP, mjMAXIMP] which is currently set to [0.0001, 0.9999]. It causes the solver to interpolate between the unforced acceleration $a_0$ and reference acceleration $a_{ref}$. The user can set $d$ to a constant, or take advantage of its interpolating property and make it position-dependent, i.e., a function of the constraint violation $r$. Position-dependent impedance can be used to model soft contact layers around objects, or define equality constraints that become stronger with larger violation (so as to approximate backlash, for example). The shape of the function $d(r)$ is determined by the element-specific parameter vector solimp.

Reference

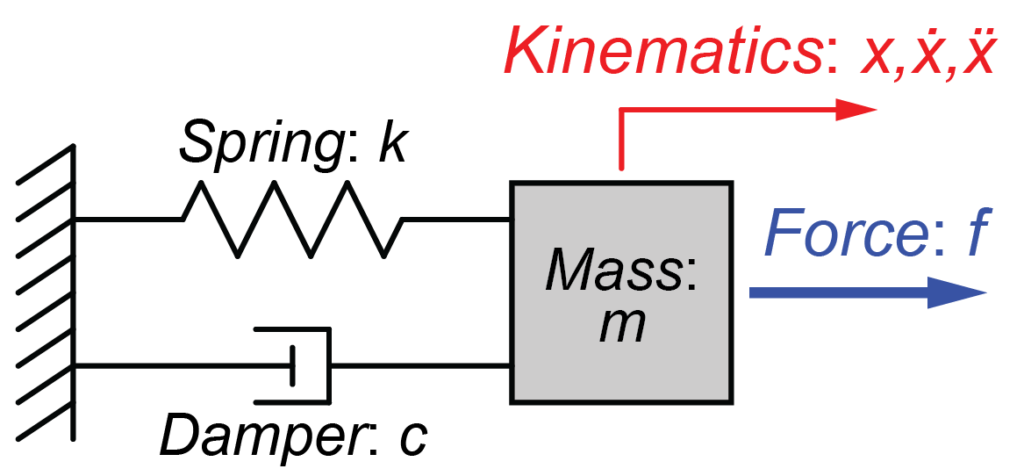
\[a_{ref} = -bv-kr\]

The reference acceleration $a_{ref}$ determines what the constraint is trying to achieve (as opposed to how well it can achieve it). This acceleration is defined by two numbers, a stiffness $k$ and damping $b$ which can be set directly or re-parameterized as the time-constant and damping ratio of a mass-spring-damper system (a harmonic oscillator). The reference acceleration is controlled by the solref attribute.

The Hyfydy and MuJoCo simulation engines differ in these key areas:

  • Musculotendon dynamics: The muscle model in Hyfydy is based on Millard at el. [59] and includes elastic tendons, muscle pennation, and muscle fiber damping. The MuJoCo muscle model is based on a simplified Hill-type model, parameterized to match existing OpenSim models [42], and supports only rigid tendons and does not include variable pennation angles.

  • Contact forces: Hyfydy uses the Hunt-Crossly [60] contact model with non-linear damping to generate contact forces, with a friction cone based on dynamic, static, and viscous friction coefficients [61]. MuJoCo contacts are rigid, with a friction pyramid instead of a cone, and without separate coefficients for dynamic and viscous friction.

  • Contact geometry: The MuJoCo model uses a convex mesh for foot geometry, while in the Hyfydy models the foot geometry is approximated using three contact spheres.

  • Integration: Hyfydy uses an error-controlled integrator with variable step size, while MuJoCo uses a fixed step size and no error control. The average simulation step size in Hyfydy is around 0.00014s (7000 Hz) for the H2190 model, compared to the fixed MyoSuite step size of 0.001s (1000 Hz) for the MyoLeg model.

references:

/*!
 * Compute actual actuator torque, given desired torque and speed.
 * takes into account friction (dry and damping), voltage limits, and torque
 * limits
 * @param tauDes : desired torque
 * @param qd : current actuator velocity (at the joint)
 * @return actual produced torque
 */
T getTorque(T tauDes, T qd) {
  // compute motor torque
  T tauDesMotor = tauDes / _gr;        // motor torque
  T iDes = tauDesMotor / (_kt * 1.5);  // i = tau / KT
  // T bemf =  qd * _gr * _kt * 1.732;     // back emf
  T bemf = qd * _gr * _kt * 2.;       // back emf
  T vDes = iDes * _R + bemf;          // v = I*R + emf
  T vActual = coerce(vDes, -_V, _V);  // limit to battery voltage
  T tauActMotor =
      1.5 * _kt * (vActual - bemf) / _R;  // tau = Kt * I = Kt * V / R
  T tauAct = _gr * coerce(tauActMotor, -_tauMax, _tauMax);

  // add damping and dry friction
  if (_frictionEnabled)
    tauAct = tauAct - _damping * qd - _dryFriction * sgn(qd);

  return tauAct;
}